M&A Blog #21 – valuation (scenario / sensitivity analysis)

Thus far, we have discussed five valuation methods: DCF, Comparable Company, Precedent Transaction, LBO, and Dividend Discount Model (DDM). In all of these discussions, we assumed a set of static values for our variables. In other words, we assumed that each variable can have only one value. Well, in the real world, there is no certainties in business. Grays exist more than black and white; multiple possibilities exist, leading to multiple outcomes. So, a good valuation model has to take into account the possibilities of a variable having multiple values along with each value’s probability of occurring. In short, a good valuation model has to include a scenario and sensitivity analysis. To-date, we have lumped them together. In this post, we will distinguish between the two, explain why they are important, the requirements and steps for each, and their advantages and disadvantages.

A scenario analysis evaluates the expected value of a proposed acquisition, investment, or business activity. By creating various scenarios that may occur, a valuation professional will be better able to determine if an expected outcome will occur. A sensitivity analysis determines how different underlying elements (independent variables) impact an expected outcome (dependent variable) under a given set of assumptions. Knowing which underlying elements need to be boosted or reduced to what level increases an acquirer’s / investor’s chance to getting the expected outcome. Both types of analyses are important because the high-stake natures of acquisitions and investments. The more an acquirer / investor knows about what outcomes to expect, how likely they are to occur, and what factors can tip the final outcome to the acquirer’s / investor’s favor; the better informed the individual is on how to structure an acquisition or investment (including if s/he should walk away from the opportunity).

To properly perform these analyses, knowledge of statistical concepts and techniques are needed. In fact these are the areas where finance and statistics intersect. At the minimum, a valuation professional should be informed about population, sampling, mean, standard deviation, standard error, different probability distributions, and binomial scenarios. While an in-depth statistical discussion about these concepts is beyond the scope of this post, I will discuss them briefly as they come up during this post.

Some of the most common scenario analysis techniques are:

1. Fixed-case scenario analysis

2. Two-variables scenario analysis

3. Monte Carlo simulations

We will also use the Monte Carlo technique to perform a sensitivity analysis.

Fixed case scenario analysis basically involve creating one base case model and then replicating it for an upside and a downside variations. In the base case model, the analyst performs the analysis with values that are most likely to occur for each supporting independent variable. In the upside model, the analyst performs the analysis with values that are likely to occur for each supporting variable if everything goes as planned to the advantage of the acquirer / investor (basically, the most positive, high outcome). The downside model adopts the opposite values (basically, the least positive, low outcome). It is worth noting that the independent variables used in all three models are the same, they just have different values for each scenario. The advantage of this approach lies on its simplicity - it is easy to model and can be performed relatively quick. The disadvantage of this approach is its inability to handle complex scenarios (when some independent variables are high and others are low); which are likelier to happen in real life compared to straight up positives or negatives all the time.

Two-variables scenario analysis basically involve creating data tables that allow a valuation professional to predict how would an outcome (dependent variable) changes given a range of values for two of its supporting (independent) variables. An example of this technique include the changes of stock value given differing:

• WACCs and long-term free cash flow growth rates.

• WACCs and EBITDA multiples.

• WACCs and long-term dividend growth rates.

Similar to the fixed case scenario analysis approach, the advantage of the two-variables scenario analysis lies on its simplicity - it is easy to model and can be performed relatively quick. The disadvantage of this approach is its inability to handle complex scenarios. In the real world, it is unlikely that only two independent variables change over time. This approach basically forces the analyst to select two independent variables that the analyst think would cause the most change on the outcome. As it relies on the analyst knowledge, opinions, and beliefs of what will happen in the future; this approach is of limited use.

Given the limitation of the first two scenario analysis approaches, we will now discuss a more robust alternative. The Monte Carlo simulation has an advantage of being able to handle complex scenarios (mixed upside/downside variables and more than two variables at a time). The disadvantage of this approach is its complexity, amount of time needed to set one up properly, and the intermediate / advanced statistical knowledge required to interpret the simulation results. Nevertheless, given the high stake nature of acquisitions and investments, I highly recommend this additional step when the due diligence process timeline allows for it.

Monte Carlo simulation is basically a technique that converts uncertainties in input (independent) variables of a model into probability distributions. By combining the distributions and randomly-selected values (within the range the analyst specifies), the simulation recalculates the model many times (5000, 10000, or more depending on the analyst’s specification) and brings out the most likely output (outcome / dependent variable). Further, a Monte Carlo simulation results include a sensitivity analysis that showcase which independent variables have the most impacts to the outcome. Overall, this technique allows the acquirer / investor to know not only what is the likely value of an opportunity, but also what independent variables need to be change about the opportunity for the acquirer / investor to get optimal returns. Of course, only some of the independent variables are within the individual’s control to change; for example: no company or individual investor has yet to be able to change the risk-free rate.

The major steps of Monte Carlo are:

1. Installing a Monte Carlo simulator.

2. Determining which independent variables within the model should be tested.

3. Deciding which probability distribution is most appropriate for each independent variable to be tested.

4. Determining the values or range of values to be associated with each probability distribution.

5. Identifying output variables and naming them properly.

6. Ensuring that the current model is properly linked to the each Monte Carlo variable.

7. Deciding the number of simulations required and run the simulations.

8. Interpreting the resulting range of outcome.

9. Interpreting the resulting sensitivity analysis.

10. Calculate the upside potential.

We will delve deeper into each steps above in the following paragraphs of this post. It is worth noting that each step can justifiably warrant an entire post in itself. For the purposes of this post though, we will keep matters concise by discussing only the most practical and commonly accepted aspects of each step.

The 1st step in Monte Carlo simulation is to install an Excel-based simulator that can work with standard MS Excel. There are many options out there, the one that I’m familiar with is Palisade’s @RISK tool. To download @RISK for a free trial version, click here. I recommending downloading and opening @RISK prior to building and working with a Monte Carlo-embedded Excel file. The file will not properly open without that step and will even open with error messages.

The next (2nd) step of Monte Carlo is to determine which independent variables within the model should be tested, including:

• Income Statement: COGS, SGA, tax expense.

• Balance Sheet: cash and cash equivalents, receivables, inventories, prepaid expenses and other current assets, Net PPE, other assets, account payable, accrued liabilities, long-term debt, deferred tax and other liabilities.

• Others: risk-free rate, market risk premium, beta, long-term GDP growth rate, EBITDA multiples, and dividend growth rate.

The 3rd step of Monte Carlo calls for deciding which probability distribution is most appropriate for the to-be-tested independent variables identified in the previous step. This is where statistical knowledge of probability distribution is required. Four of the most frequently used probability distributions are:

• Triangular Distribution: continuous distribution with fixed minimum and maximum values. This bounded distribution can be symmetrical or asymmetrical, allowing values to be designated least and most likely to occur.

• Uniform Distribution: continuous distribution also bounded with minimum and maximum values. Unlike its triangular cousin, this distribution assigns the same likelihood of occurrence between the minimum and the maximum.

• Lognormal Distribution: continuous distribution specified by mean and standard deviation. It is appropriate for a variable ranging from zero to infinity.

• Exponential Distribution: continuous distribution used to illustrate the time between independent occurrences, given a rate of occurrence.

Because of the limitations of the lognormal and exponential distributions, I only use the triangular and uniform distributions in my valuation models. @RISK’s RiskTriang and RiskUniform functions capture these distributions perfectly.

The next (4th) step of Monte Carlo is to determine the values or range of values to be associated with each independent variable’s probability distribution. An example of this step is: if we know that Net PPE will fluctuate between 0.74% to 1.61% of sales with 1.18% being the most likely percentage, we would select 0.74%, 1.18%, and 1.61% for Net PPE’s RiskTriang function in our Monte Carlo model. Similarly, if we know that the EBITDA multiple that we chose will fluctuate between 7.26x and 9.72x and all of the values in between are equally likely, then we would choose 7.26 and 9.92 for our model’s EBITDA multiple’s RiskUniform distribution. Obviously, which probability distribution and which range of values we choose depend on our understanding of each independent variable and our expectation of its likely value.

The 5th step of Monte Carlo calls for identifying the output variables (dependent variables) and naming them properly. Monte Carlo simulators are very advanced these days, but they still need to be told what is it that we are testing and where the test results should be focused on. Identifying the output variables and naming them properly help the simulator decide where the analysis should be done. For the purpose of our post, the output variables should be the per-share equity value returned from our DCF, Comparable Company, etc. valuation exercises. Other common outputs are equity value and enterprise value.

The next (6th) step of Monte Carlo is to inspect: making sure that our current model is properly linked to each Monte Carlo variable. This is a simple step that is often overlooked, but it is critical. As Monte Carlo models are complex, it is common for variables to be “broken” (not properly linked) anymore. Spending some time to check and make sure that all of the variables are still linked to the correct source is a good investment of time.

The 7th step of Monte Carlo is to decide the number of simulations to be run and to run the simulations. Common numbers are 1000, 5000, and 10,000. Of course, one is free to choose other numbers. The key here is to select a large enough number so that the test will be meaningful, yet not too large that simulations take forever to finish. Once the number is selected and the simulation is run, it might take a few minutes for the simulations to finish.

The next (8th) step of Monte Carlo is to interpret the resulting range of outcome. For this step, we look at the mean and standard deviation of the resulting probability distribution graph. Using these information, we proceed in our calculation as follow:

• Standard Error: Standard Deviation / the square root of the number of simulations.

• 90% Confidence Interval - Lower Bound: Mean - 1.96 * Standard Error.

• 90% Confidence Interval - Upper Bound: Mean + 1.96 * Standard Error.

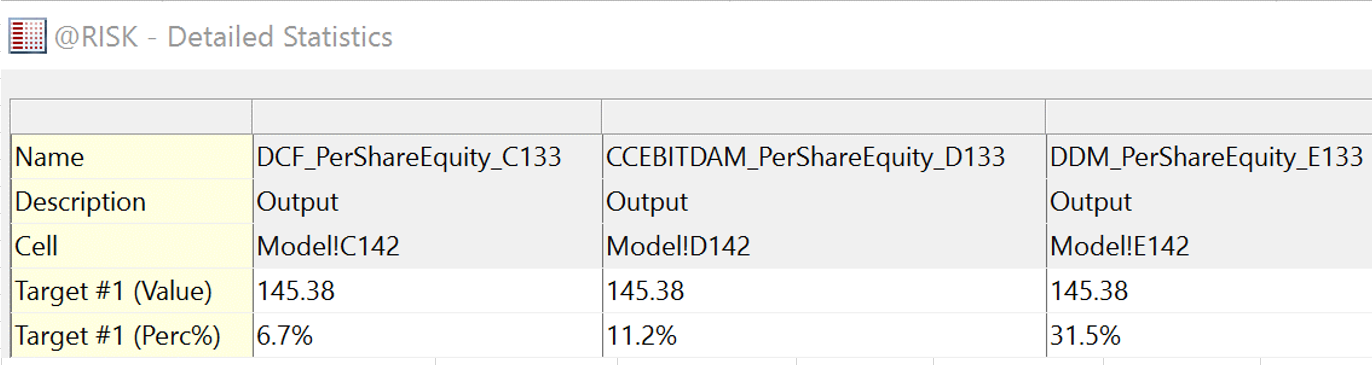
The lower and upper bound of the 90% confidence interval form a range of values that are the likeliest range of values for our designated output. Meaning, if we are testing for per-share equity value and these numbers turned out to be $265 and $279, that means that, based on our inputs so far, the justifiable, theoretical stock price should be between $265 and $279. The narrower this range turns out to be, the better it is for our valuation exercise.

The 9th step of Monte Carlo is to interpret sensitivity analysis. For the sensitivity analysis, the regression map (above) tells us the variables that impact our model the most, based on their magnitude of impact. Left-leaning bars denote when a variable has a reverse (negative) relationship with the output variable, and right leaning bars denote when a variable has a positive relationship with the output variable. For example, in the map above, any additional increase in Market Risk Premium causes a negative drop in stock price and any additional increase in long-term GDP growth rate causes a positive increase in stock price. This sensitivity analysis is helpful because acquirers can decide to use the information to change some of the elements within acquirer’s control (SGA / COGS) post acquisition to get to a better outcome. For investors, it provides useful information on what has to change about the company or its operating environment (risk-free rate, market risk premium, etc.) for a higher return. If an investor believes that risk-free interest rate is about to increase / decrease, s/he might choose to act differently about an opportunity, everything else held constant.

The 10th and final step of Monte Carlo is to calculate the upside potential, a step popular with stock pickers and investors. Sophisticated Monte Carlo simulators often come with a functionality to showcase the probability of a specific value for an output variable. Meaning, if we know that our stock price should be between $265 and $279 and the current market stock price is $145, we can ask our Monte Carlo model to tell us what percentage of its simulation has yielded $145 or less (i.e. how likely is it that the stock price is that low?). We already know that the current market stock price is undervalued, the Monte Carlo’s answer will tell us by how much. Further, we can calculate the likelihood that the current market stock price will go up in the future by the following calculation:

• Upside potential = 1 - the percentage of simulation results where the output variable (theoretical stock price) is equal to or less than the current market stock price.

For example, in the above graph, we see that based on our DCF model, the current market stock price of $145.38 is returned in 6.7% of our simulations. That means, there is a 93.3% chance (derived from 1 - 6.7%) that the current market stock price will increase in value in the future. It is a strong indicator that the current market is undervaluing the stock. For an even better result, repeat this upside potential calculation with the other valuation models’ results and compare the answers. If a majority or all of the models show high, positive upside; there is a very strong chance that the current market stock price is undervalued.

A sample file for a Monte Carlo simulation on the company McKesson can be accessed here; it is recommended to open @RISK first before opening this file due to the Monte Carlo simulation embedded in this file (the file will open with errors without @RISK). To download @RISK for a free trial version, click here

So, to recap, we have discussed what scenario and sensitivity analyses are, why they are important, and the approaches that can be taken to undertake them. We have talked about the fixed-case approach, the two-variable approach, and the Monte Carlo approach; along with advantages and disadvantages of each. We have also walked through the major steps of Monte Carlo analysis and how to interpret the results. It is important to remember that a Monte Carlo analysis is only as good as the valuation model it is based on (the underlying DCF, Comparable Company, etc. models). If the underlying model is bad, then the Monte Carlo analysis is useless. On that note, I would wrap up this post by noting that our next post on other valuation methods will be our last valuation post before we head onto the next M&A topic: due diligence.